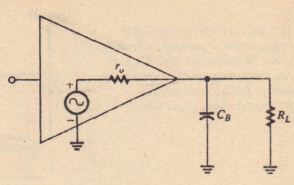
Figure 10-18 shows shunt capacitance Co connected across the output of an amplifier. The output resistance R of the amplifier. the load resistance RI and the capacitance CL form a low-pass RC network that has the same effect on the high frequency response as the low-pass network at the input: the gain falls off because the impedance to ground decreases with increasing frequency. The upper cutoff frequency due to C8 is derived in the same way as that due to C Hereafter, we will distinguish between the two frequencies by using the notation h( CIl) and h( C8):
When there is shunt capacitance at both the input and the output of an amplifier. the frequency response is different than it would be if only one were present. If h(C) and h(CB) are not close in value, then the actual upper cutoff Frequency is approximately equal to the smaller of h(CA) and(C). The gain is asymptotic to a line that falls off at 20 dB/decade (6 dll/octave) between the smaller of(C,d
and f;( en) and is asymptotic to a line that falls off at 40 dls/dccude (12 dB/octave) at frequencies above the larger of the two. See Figure lO-l9(a). At the higher frequencies. the gain falls off at twice the rate it would for a single low-pass network, because both eA and Cn contribute simultaneously to gain reduction. The total phase shift approaches -IRO° at high frequencies. The exact value the upper cutoff frequency in terms of d and e can be found From (Appendix C) If C= f(C/J) = f, equation 10-32 can be used to show that the cutoff frequency is = 0.645f In that case, there is but one.break Frequency > f (C,I) = ( C). and the single asymptotic has slope 40 or 12 dB/octave. See Figure 1O-19(b). When the two [rcquencies arc equal’ 1,;11 phase shift is -900
at that frequency.
Thevenin Equival~nt Circuits at Input and Output
We note that the’ same [on of equation is used to compute both the lower and upper cutoff frequencies of an amplifier: f = 1/21TRC. In the case of!t, C is either
input or output coupling capacitance and in the case of /2, C is input or output shunt capacitance. In both cases, R is the Thevenin equivalent resistance seen by the capacitance. This observation provides an easy way to remember the equations for calculating t, and wherefore 1\11 is the Thevenin equivalent resistance with respect to the capacitor terminals at input or output. Figure 10-20 illustrates this point. Recall that the Thcvernn equivalent resistance is found by open-the capacitor terminals and com-
punting the total equivalent resistance looking into those terminals when all voltage sources are replaced by short circuits. Figure 10-20(a) shows how equation 10-33 is applied to calculate the lower cutoff frequency due to input coupling capacitance, C” and Figure 1O-20(b) shows how the equation is applied to calculate the upper
cutoff frequency due to output shunt capacitance, C As an exercise. verify that the equations for (C) and j;( c,.) can also be found using the Thevcnin equivalent resistance with respect to the capacitor terminals.
Miller-Effect Capacitance
Figure /0-21 shows an amplifier having capacitance Cc connected between its input and output terminals. The most common example of such capacitance is interrelation capacitance, as, for example, between the base and the collector of a common-emitter amplifier or between the gate and the ‘drain of a common-source amplifier. This capacitance forms a feedback path for ac signals and it can have a
significant influence on the high-frequency response of an amplifier.
The conclusion in the derivation that follows is based on the method used i circuit analysis to determine the total admittance (y) of components connected in parallel, which we will review briefly now. Recall that admittance is the sum of conductance 8 and acceptance b: y = g + jb Siemens. Also recall that the total admittance of parallel-connected components is the Sill of their individual admittance. The acceptance of capacitance C is b =C S. In particular, the to Figure 10-21 Capacitance C· connected between the iI/- put and the output of (/1/ amplifier affects its high-frequency response due to the Miller effect.Thus, for example, if the input admittance to a circuit were 0.01 + O.02 S at frequency w = 1000 rails, we would conclude that the input circuit consisted of resistance R = l/g = 1/0.01 = 100 n in parallel with capacitance C = 0.021 lOOO == 20 Writing Kirchhoff’s current law at the node labeled A in Figure 10-21, we have