Low-Frequency Response of FET AmpUfiers
Figure 10-35 shows a common-source JFET amplifier biased using the combination of self-bias and a voltage divider as studied in Chapter 7 For our purposes now the PET could also be a MOSFET. The capacitors that affect the low-frequency Figure W The lowfrequency response of an FET amplifier is affected by capacitors.
response are the input coupling capacitor, CI, the output coupling capacitor, Q and the source bypass capacitor, Cs. Applying equations 10-40 and 10-4] to this amplifier configuration, we Iind where r; =(stage) = rd II R/J. The bypass capacitor C, affects low-Irequcncy response because at low frequencies its reluctance is no longer small enough \0 eliminate degeneration. The cutoff frequency due to C, is the frequency at which the reluctance of C,equals the resistance looking into the junction of R, and C, at the source terminal namely Thus,Since the bias resistors R, and R2 are usually very large in FET amplifier, the input coupling capacitor C, can be smaller than its counterpart in a BJT CE amplifier, and C, does not generally determine the low-frequency cutoff. The small value of R makes the source bypass capacitor the most troublesome. in that a large amount of capacitance is required to achieve a small value of (Cs).The FET shown in Figure 10-36 has gill = 3.4 mS and r,/ = 100 k Find the approximate lower cutoff frequency.
Figure 10-37 shows JFET and MOSFET amplifiers in the common-drain (source-follower) configuration and gives the equations for (CI) and n( C2). These equations arc obtained in a straightforward manner using the same low-frequency theory we have discussed for general amplifiers. For-design purposes, each of the equations for .fi( CI), fie Cl), or fl( Cs) in each of the three configurations is easily solved for CI, C2, or Cs, giving a set of capacitor equations similar to equations 10-44 through 10-46.
High-Frequency Response of FET Amplifiers
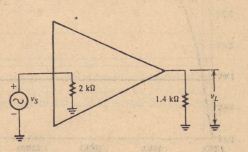
Like the BJT common-emitter amplifier, the FET common-source amplifier is affected by Millet capacitance that often determines the upper cutoff frequency. Figure 10-38 shows a common-source amplifier and the inter electrode capacitance that affects its high-frequency performance. Since R, is completely bypassed at high
frequencies, Cp and Cds are effectively shunting the input and output, respectively, to ground. The equations for h(C,I) and fi( CH) are obtained directly from the general high-frequency-cutoff theory we have studied:
The JFET in Figure 10-38 has = 3.2 mS. = CK> = 4 pF = O.S pF. and CKd = 1.2 pF. The wiring capacitance shunting the input is 2.5 pF and that shunting the output is 4 pF The component values in the circuit are
circuit file. The MOSFET transistor has VTO = 2 and KP = O.SE-3. Let other parameters default. Solution. The Spic circuit and input circuit file are shown in Figure lO-40(b). A plot of the voltage across the load resistance, V(7), as displayed by Probe, is ‘shown in Figure IO-40(c). We see that the maximum load voltage is 2.5 V. Therefore, the lower and upper cutoff frequencies occur where the load voltage is 446 Frequency Response 0.707(2.5 V) = 1.767 V. As shown in the Probe display, cursor Cl is moved to a point on the plot where the. voltage equals 1.7672 V, and we see that the lower
cutoff frequency is 1.4342 kHz. C2 IS moved to 1.7667 V at the high-frequency end of the plot, and we;see that the upper cutoff frequency is 8.0475 MHz amplifier is 120 kHz and its upper cutoff frequency is I MHz. The peak-to-peak output voltage in the midland frequency range is 2.4 V p-p and the output power at 120 kHz is 0.4 W. Find a. the bandwidth, b, the rms output voltage at I MHz, c. the output power in the midband frequency range, and d. the output power at I MHz. . 10-2. The voltage at the i”l,ul of an amplifier is IS mV rms. The amplifier delivers 0.02 Arms to a 12-11 load at 1 kHz. The input resistance of the amplifier is 1400 n. Its lower cutoff frequency is 50 Hz and its bandwidth is 9.95 kHz. Find a. the upper cutoff frequency, 11; b. the output power at 50 Hz; c. the power gain; and d. the power gain at /2’ 10-3. The input signal to a certain amplifier has a I kHz component with amplitude 0.2 V rms and a 4-” Hz component with amplitude 0.05 . In the amrs output, the component has amplitude 0.5 V rms and is .Cyclades with respect to the I-kHz input component hy 0.25 ms. If the output is to he an version of the input, what should be the amplitude and delay of the 4-kHz output component? Section 10-2 Decibels and Logarithmic Plots 111-4. Find the power gain 10-5. A certain amplifier has a power gain of 42 dB. The output power is 16 Wand the input resistance is 1 kU. What is the rms input voltage? the output voltage is b.X V Grus, and the input and load resistances both equal RO U, find a. the input voltage; and b. the power gain in decibels. 10-10. The output voltage of an amplifier is 12.5 dl above its level at point in the amplifier. The amplifier input voltage is 6.4 dB below the voltage at point If the output voltage is 2.4 V rms, find