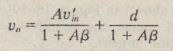Harmonic Distortion
Recall that any periodic waveform sinusoidal or otherwise, can be represented as the sum of an infinite number of sine waves having different amplitudes Ire and phase relations. The mathematical technique called Fourier analysts is concerned with finding the exact amplitudes frequencies and phase angles of the sine wave components that reproduce a given waveform when they are added together. Of course, if the waveform is itself a pure sine wave, then all other frequency components have zero amplitudes.
Apart from a possible de component (the average value), the lowest frequency component in the infinite sum is a sine wave having the same frequency as the periodic waveform itself. This component is called the fundamental and usually has. an amplitude greater than that of any other frequency component. The other frequency components are called harmonics, and each has a frequency that is an integer multiple of the fundamental frequency. For example, the second harmonic of a 3-kHz waveform has frequency 6 kHz, the third harmonic has frequency 9 kHz, and so forth. Not all harmonics need be present. For example, a square wave conains only mid harmonics (third, fifth, seventh, etc.).
Special instruments, called distortion analyzers, are available for measuring the total harmonic distortion in a waveform
Example 16-8
Tue principal harmonics in a certain 15-kHz signal having a 10-Vpk fundamenta. are the =econd and fourth. All other harmonics are negligibly small. If the THO 1 12% and tl ‘- amplitude of the second harmonic is 0.5 V pk, what is the attribute of the 60 kHz harmonic?
Solution
Using Negative Feedback to Reduce Distortion
We have mentioned in several previous discussions that one of the importan. benefits of negative feedback is that it reduces distortion caused by amplifier non earities. Having defined a quantitative measure of distortion, we can now undertake a quantitative investigation of the degree to which feedback affects harmonic distortion in the output of an amplifier. Let us begin by recognizing that a nonlinear amplifier is essentially an amplifier whose gain changes with signal level. Figure 16-19(a) shows thl. transfer characteristic of an ideal, distortion less amplifier, in which the gain, i.e., the slope of the characteristic, A V..!t. Vin = 50, is constant. Figure t 6-19(b) shows a nonlinear transfer characteristic in which the slope, and hence the gain, increases with increasing signal level. We see that the gain at VUI = 0.2 V is 50, while the gain at 0.4 V is 100. There is a 1009’0 increase in gain over that range, so serious output distortion is to be expected.
In earlier discussions of negative feedback, we showed that the closed-loop gain An. of an amplifier having open-loop gain A and feedback ratio f3 can be found from
Let us suppose we introduce negative feedback into the amplifier with the nonlinear characteristic shown in Figure 16-19(b). Assume that I’ = 0.05. Then the gain at ViII = 0.2 V becomes
and the gain at Vm = 0.4 V becomes
‘a) Transfer characteristic of an ideal, distorlion less amplifier having gain 50
Nonlinear transfer characteristic
(c) Negative feedback reduces the gain but linearizes the characteristic
Transfer characteristics and the effect of negative feedback
To compute the reduction in harmonic distortion caused by negative feedback consider the models shown in Figure 16-20. Figure 16-20(a) shows how amplifier distortion (without feedback) can be represented as a distortion less amplifier having a distortion component d added to its output. For example, d could represent the level of a second-harmonic sine wave added to an otherwise undistorted fundamental. The output of the amplifier is
so the harmonic distortion is
Figure 16-20(b) shQws the amplifier when negati •.e. feedback is connected. We realize that the negative feedback will reduce the closed-loop gain, so the output level will be reduced if Vin remains the same as in (a), But, for comparison purposes, we want the output levels in both cases to be the same since the amount of distortion depends on that level. Accordingly, we assume that Vln in (b) is increased to »i; as necessary to make the distortion component d equal to its value in (a). As shown in the figure,
(a) Amplifier distortion represented by summing a distortion component with the amplifier output
b) Model for an amplifier with distortion component d and feedback ratio 13
Amplifier distortion models
Solving for v,,, we find
When we adjusted v'” to v’: we did it so that the amplifier outputs in (a) and (b) of the figure would be the same
or
Substituting (16-57) into (16-55), we fine
The harmonic distortion is now
Comparing with equation 16-53, wc see that the distortion has been reduced by the factor 1/( I + A(3)
I.t is important to remember that it was necessary to increase the input level in our analysis to achieve the improved perfor=once. From a practical standpoint. that means that a relatively distortion-free pre amplifier must be used to compensate for the loss in gain caused I1y negative feedback around the output amplifier. Fortunately, it is generally easier to achieve low distortion in small-signal prcarnplifiers than in large-signal, high-power output amplifiers
Example 16-9
An output amplifier has a voltage gain of 120,and generates 20% harmonic distortion with no feedback.
1. How much negative feedback should be used if it is desired to reduce the distortion to 2%?
2. How much pre amplifier gain will have to be provided in cascade with the output amplifier to maintain an overall gain equal to that without feedback?
Solution
1. From equation 16-59,
where dlAvill = 0.2 is the distortion without feedback. Then,
or {3 = 0.075. Thus, the negative feedback voltage must be 7.5% of the output voltage .
2. r- he closed-loop gain with 7.5% feedback is
To maintain an overall gain of 120, the preamplifier gain, Ap, must be such thai . 12A. = 120, or Ap = 10.