Recall from that one of the chnrnctcristi.cs of an ideal operational amplifier is that It has zero output voltage when both inputs are 0 V (grounded), This chaructoristic is p~rHc~larly importa~t in appllcations .where de or 19 w-frequency signals arc . If the output IS not 0 :when ~he inputs . then the output will not he lit Its correct de level when the Input IS n de level other than O. The actual value of the output voltage when the: inputi tire 0 is called the output off.·,( cottage. Output offset is very much like a de bins level in the output of a converuioual amplifier in that it is added to whatever signal variation occurs there, If an operation1 amplifier ·is used only for ac signals, it can be capacitor-coupled if necessary or desirable to block the de component re~~osentQd by the;’ offset. However, the capacitors may have to be large if low frequencies and small impedance levels are Involved. Alse, 0 de path must always be present between each input and ground to allow bias currents to flow. Small offsets, on the order of a few millivolts, CUll oftlJll be ignored if the signal variations are large by cornparison. On the other hand, a frequent application of operational amplifiers is in precise, high-accuracy signal processing at low levels and low frequencies, and in these situations, very small offsets are crucial.
Manufacturers do not generally specify output offset because, as we shall see, the Of(lit;t level depends on the closed-loop gain that a user designs through choice of external Ctlmpm/!nt values. Instead, input offsets are specified, and the designer can use these values to eompute the output offset that results in a particular application, Output offset voltages are the result of two distinct input phen rnena: input bias currents and input offset voltage. We will use the supcrpositioi principle to the contribution of each of these input effects to the output offset voltage.
Input Offset eurrent
In our discussion of differential amplifier circuits in Chapter 12, we ignored base currents because they hod negligible effects on the kinds of computations that held our interest then, We know that some dc base current must flow when a transistor is properly biased, and, although small, this current flowing through the external resistors in an amplifier circuit produces a de input voltage that in turn creates an output offset.
To reduce the effect of bias currents, a compensating resistor R, is connected in series with the noninverting (+) terminal of the amplifier. (K must provide a dc path to ground, so if a signal is capacitor-coupled to the + input, R; must be connected between the + input and ground.) We will presently show that proper choice of the value of R, will minimize the output offset voltage due to bias current, Figure 13-25 shows the bias currents It and I/j flowing into the + and – terminals of an operational amplifier when the signal inputs are grounded. While the bias currents may actually flow into or out of the terminals, depending on the type of input circuitry, we will, for the sake of convenience, assume that the directions are is shown and that the values are always positive. These assumptions will not affect our ultimate conclusions. The figure also shows the compensating resistor R•.connected in series with the + terminal. Note that this circuit applies to both the inverting and noninverting configurations.
The equivalent circuit of Figure .13-25. Here, the bias currents are represented by current sources having resistances R, and R… the same circuit when the current sources are replaced by their Thevenin equivalent voltage sources
Using Figure 13-26(b), we can apply the superposition principle to’ determine the output offset voltage due to each input source acting alone. As illustrated in Figure 13-27(a), the amplifier acts as an inverter when the source connected to the + terminal is shorted to ground, so the output due.
When the source connected to the terminal is shorted to ground, the amplifier is in a noninverting configuration, so the output due to lyRc.
Depending on which of the terms on the left side of equation U-S4 is greater, VO.l'(IIi) may be positive or negative, However, the sign of VoS(ln) is of little interest, since negative offset voltage is just as undesirable as positive offset voltage, Our real interest is in finding a way to minimize the magnitude of VO.l'(/II)’ Toward that end, let us make the reasonable assumption that the two inputs arc closely matched and that, as a consequence, they have equal bias currents: It = [/j = [/In’ Substituting.
If the expression enclosed by the brackets in (13-55) were equal to 0, we would have zero offset voltage. To find a value of R, that accomplishes that goal, we set the bracketed expression equal to °and solve for R
Equation 13-56 reveals the very important result that output offset due to input bias currents can be minimized by connecting a resistor R;. having value series with tile noninoerting input. This method of offset compensation is valid for both inverting and non inverting configurations. Notice that we say the offset can be minimized using this remedy, rather than being made exactly 0, because the remedy is based on the assumption that It. = tn. which may not be entirely valid. We can compute the exact value of VOS(/II) when R, = RI II R, by substituting this value of R, back into (13-54), where the a.ssumption is not in force:
Equation 13-57 shows that the offset voltage is proportional to the difference between IJi and In when R R, II Rf. Since the inputs are usually reasonably well matched, the difference’ etween Ik and In is quite small. The equation confirms the fact that Vos is 0 if IJi exactly equals Is. The quantity IJi – Iii is caIled the input offset current and is often quoted in manufacturers’ specifications. Remember that it is actually a difference current. Letting the input offset current n – to be designated by Ii,,, we have, from equation 13-57.
Vos(Ju) may be either positive or negative. depending on whether Just; or vice versa. Unless actual measurements are made, we rarely know which current is larger. so a more useful form of (13-58)
Manufacturers’ specifications always give a positive value for Ii”, so it is best interpreted as an absolute value in any case. .
Equation 13-59 shows that the output offset is directly proportional to the value of the feedback resistor Rf• For that reason, small resistance values should be used when offset is a critical consideration. However, to achieve large voltage gains when Rf is smaIl may require impractically smaIl values of R to the extent that the amplifier may load the signal source driving it. In any event, large closed loop gains are detrimental to another aspect of output offset, as WI.: will see in a fort hcorning discussion.
Another common manufacturers’ specification is called simply inpu! bias cur- 1′(‘111. 1/1. By convention. 1/1 is the aurrag« of I,’, and 1/1:
1/1 is typically much larger than I,.. because 1/1 is on the same order of magnitude as nand 1/1. while I”. is the difference between the two. Given values for 1/1 and I,,,, we can rind 1/, and 1/1, provided we know which is the larger. If !J, > I,f. then
If 1/1 > n, the + and – signs between terms in (13-61) are interchanged. Proof of these relations is left to Exercise 13-44 at the end of the chapter.
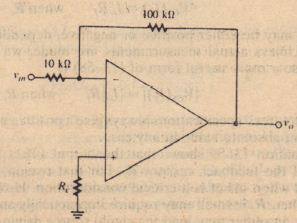
The specifications for the operational amplifier in Figure 13-28 state that the input
bias current is HO nA and that the input offset current is 20 nA.
1. Find the optimum value for R,.
2. Find the magnitude of the output offset voltage due to bias currents when R.. equals its optimum value.
3. Assuming that n > 1/1, find the magnitude of the output offset voltage when R, = O.
SOLUTION
Input Offset Voltage
Another input phenomenon that contributes to output offset voltage is an internalfy generated potential difference that exists because of imperfect matching of the input transistors. This potential may be due, for example, to a difference between the VIII: drops of the transistors in the input differential stage of a BJT amplifier. Called input offset voltage, the net effect of this potential difference is the same asif a small de voltage source were connected to one of the inputs. the equivalent citcuit of an amplifier having its signal inputs grounded and its input offset voltage, Vi,,, represented as a de source in series with the noninverting input. The effect is the same whether it is connected to the inverting or non inverting input. The polarity of the source is arbitrary, because input and output offsets may he either positive or negative. Once again, it is the magnitude of the offset that concerns us. From , it is apparent that the output voltage when the input is Vi” is given by
where VCJ.I(Vi ) is the output offset voltage due to Vi,,’ Note that the compensating resistor R, is shown in Figure D-2lJ for completeness’ sake. but i1 has no effect on the output offset due to Vi,,’ Equation !J-(J2 shows that input onset is magnified at the output by a factor equal to the closed-loop gain of the noninverting amplifier, as we would expect. If the amplifier is operated open-loop, the very large openloop gain acting on the input offset voltage may well drive the amplifier to one of its output voltage limits. It is therefore important to have an extremely small Vi” in any application or measurement that requires an open-loop amplifier. Equation 13-62 is also valid for an amplifier in an inverting configuration. In fact, for a wide variety of amplifier configurations, it is true that
Vos( Vi.,) = V”,I{3
The specifications for the amplifier in Example 13-14 state that the input offset voltage is 0.8 mV. Find the output offset due to this input offset.