The transient response of an electronic amplifier or system is the output waveform that results when the input is a pulse or a sudden change in level. Since the transient response is a waveform, it is presented as a plot of voltage versus time, in contrast to frequency response, which is plotted versus frequency. Figure 10-23 shows a
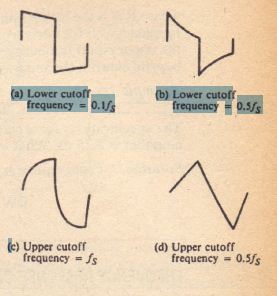
typical transient response. The transient response of an amplifier is completely dependent on its frequency response, and vice versa. In other words, if two amplifiers have identical frequency responses. they will have identical transient responses. and vice versa. A pulse can be regarded as consisting of an infinite number of frequency components. so the transient waveform represents the amplifier’s ability (or inability) to amplify all frequency components equally and to phase-shift all components equally. Theoretically, if an amplifier had infinite bandwidth, its transient response would be an exact duplicate of the input pulse. It is not possible for an amplifier to have infinite bandwidth, so the transient response is always a distorted version of the input pulse. It is necessary for an amplifier to have a wide bandwidth (to be a widemouthed, or broadband, amplifier) in order for it to amplify pulse or square-wave signals with a minimum of distortion. Square-wave testing is sometimes used to check the frequency response of an amplifier, as shown in Figure 10-24. The figure shows typical waveform that result when a square wave is applied to an amplifier whose frequency response causes attenuation of either low- or high-frequency components. “Low” or “high” frequency in any given case means low or high in relation to the square wave frequency, fl” As a concrete example of how frequency response is related to transient response, consider the low-pass RC network shown in Figure 10-25. The figure shows the output transient when the input is an abrupt change in level (called a step input), such as might occur when a voltage is switched into the network. Recall that the time constant, 7′ = RC seconds, is the time required for the transient output to reach 63.2% of its final value. Also recall that the upper cutoff frequency of the network is /2 = 1I(21TRC) Hz. Thus, /2 = 1/(2177′) Hz. Since the network passes all frequencies below /2, down to de, its bandwidth equals h – 0 = f2′ Summarizing,
Figure 10-24
Typical Oil/puts resulting [ROM square wave testing of an amplifier. J~= frequency. III (a) and (b), only low frequencies are attenuated, and ill (c) and (d), only high frequencies are attenuated.
In both cases, the attenuation outside cutoff is 20 dB/decade. (a) Lower cutoff frequency = Strolls (b) Lower cutoff frequency = O. Sls
This equation shows that the cutoff frequency and the bandwidth, which are frequency response characteristics, are inversely proportional to the time constant, which is a characteristic of the transient response. It is generally true for all electronic devices that the time required for the transient response to rise to a certain level
is inversely proportional to bandwidth. Recall that rise time, I” is the time required for a waveform to change from 10% of its final value to 90% of its final value. A widely used approximation that relates the rise time of the transient response of an amplifier to its bandwidth is
Figure 10-2$ Relationship between transient response and frequency response. Note that the bandwidth is inversely proportional to the time constant of the transient.